Context: Renewable resources such as wind and solar power are characterized by an inherently unpredictable supply. Much of this uncertainty is revealed close to real time, while planning decisions which related to the commitment of adequate generating resources for ensuring reliable system operation must be reached in day-ahead operations. This is an appropriate context for the application of stochastic programming models, which inform policy and operational models, but can be computationally cumbersome. The power industry has a lond-standing history as a prime area of application of stochastic programming methods, and energy applications have been a fertile testing ground for decomposition algorithms with applications in power systems operational planning.
Stochastic unit commitment: The unit commitment problem is the problem of determining the on-off schedule of generators in day-ahead operations, so as to serve load at minimum cost while ensuring acceptable reliability of service to electricity consumers. The determination of reserve requirements (also referred to as reserve dimensioning) is an important but difficult task, since it amounts to a delicate exercise of trading off reliability against cost of committing the resources that ensure reliable operations. Stochastic models of unit commitment can inform this process, both for the purpose policy analysis, as well as in the context of decision support for actual operations. The advantage of stochastic formulations is an endogenous representation of uncertainty (e.g. renewable supply forecast errors of generation/transmission outages, i.e. composite reliability). However, scenario selection is an important challenge in such models, since one aims at representing as few relevant scenarios as possible to arrive to an efficient decision while keeping the size of the unit commitment problem manageable. Even with a manageable number of scenarios, special-purpose decomposition algorithms (see right panel in the figure below) are required for solving the problem.

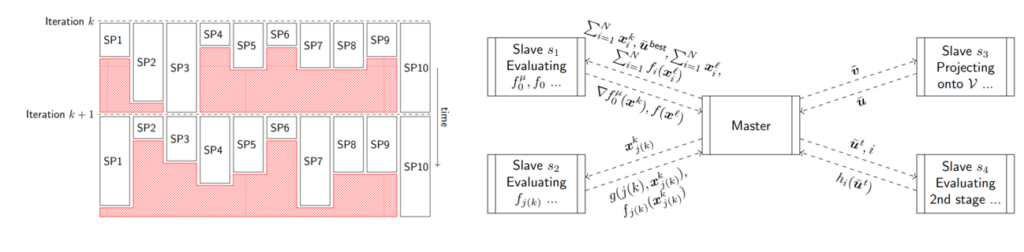
Parallel and high performance computing: Decomposition methods are needed in order to tackle the large-scale optimization problems that emerge from stochastic programming. An important appeal of decomposition algorithms is that the computational work can be distributed over multiple processors. Original implementations of such algorithms within our team in the context of stochastic unit commitment required one week of run time on 1000 processors to tackle reduced models of the Western US grid. This slow run time was in part due to synchronization delays, as indicated in the left panel of the figure below. Our team has since developed asynchronous algorithms on high performance computing infrastructure (see right panel of the figure below) that are capable of tackling instances of the Central Western European system over 1000 scenarios within 2 hours of run time by utilizing computational resources more efficiently.
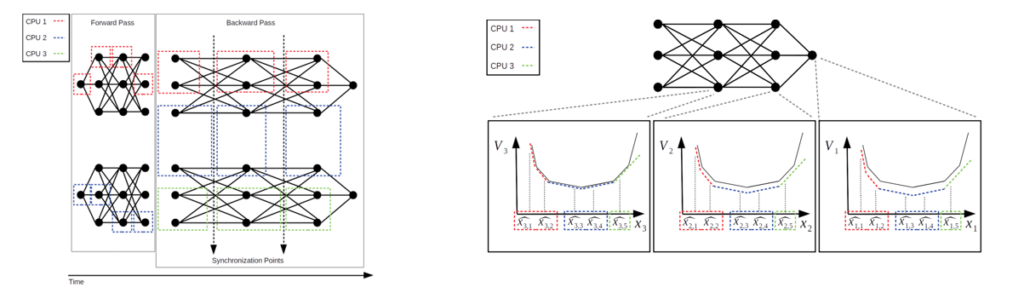
Stochastic dual dynamic programming: Parallelization and distributed computation can also be applied to the stochastic dual dynamic programming (SDDP) algorithm. SDDP is an industry standard for solving medium-term hydrothermal planning problems, where the goal is to plan on the level of storage in hydro reservoirs over multilpe months of system planning. Our team has been considering parallelization schemes for the SDDP algorithm (left panel of the figure below), as well as parallelization schemes for alternative schemes inspired by SDDP (right panel of the figure below). The alternative schemes that we are exploring aim at improving the performance of the algorithm by exploiting parallel computation in order to build tighter apprroximations of the dynamic programming value functions, which are the key building block of the algorithm.
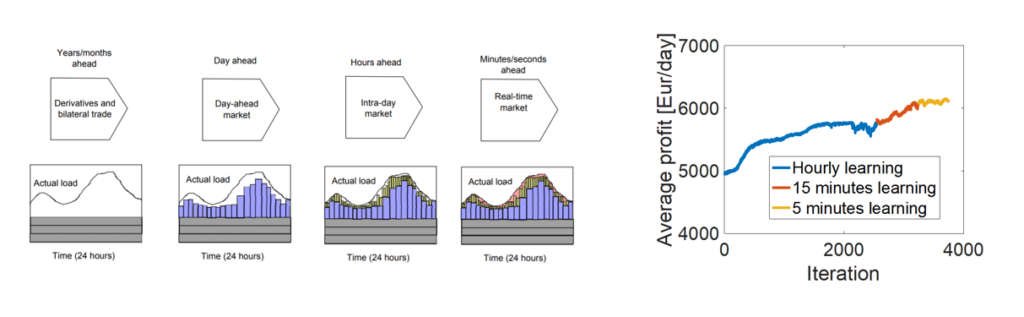
Application of reinforcement learning to intraday trading: The latest market available before delivery time in Europe is the continuous intraday market, as indicated in the left panel of the figure below. This market is therefore an attractive trading outlet for flexible assets. Trading in this market is challenging due to the multistage nature of the problem, its high uncertainty, and the fact that decisions need to be reached rapidly, in order to lock in profitable trades. Our team has been working on modeling the intraday trading problem using the Markov Decision Process framework and solving it using Reinforcement Learning. Tests in the German intraday market exhibit superior performance of the developed method (see right panel of the figure below) to the Rolling Intrinsic strategy which is employed in practice.
Read more
I. Aravena, A. Papavasiliou, Asynchronous Lagrange Scenario Decomposition, Mathematical Programming Computation, forthcoming
G. Bertrand, A. Papavasiliou, Adaptive Trading in Continuous Intraday Electricity Markets for a Storage Unit, IEEE Transactions on Power Systems, vol. 35, no. 3, pp. 2339 – 2350, May 2020
A. Papavasiliou, S. S. Oren, B. Rountree, Applying High Performance Computing to Transmission-Constrained Stochastic Unit Commitment for Renewable Penetration, IEEE Transactions on Power Systems, vol. 30, no. 3, pp. 1690-1701, May 2015
A. Papavasiliou, S. S. Oren, Multi-Area Stochastic Unit Commitment for High Wind Penetration in a Transmission Constrained Network, Operations Research, vol. 61, no. 3, pp. 578-592, May/June 2013, INFORMS Best Paper in Energy Award for 2015
A. Papavasiliou, S. S. Oren, R. P. O’Neill, Reserve Requirements for Wind Power Integration: A Scenario-Based Stochastic Programming Framework, IEEE Transactions on Power Systems, vol. 26, no. 4, pp. 2197-2206, November 2011